Un enseignement explicite associé à l’utilisation des problèmes résolus comme stratégie fondamentale est l’approche la plus appropriée pour l’apprentissage du raisonnement et des stratégies en algèbre.
(Photographie : Rob Hann)
Charge cognitive des apprentissages en algèbre
Par rapport à des contenus mathématiques élémentaires comme l’arithmétique, la résolution de problèmes d’algèbre exige des élèves qu’ils pensent de manière plus abstraite.
Le raisonnement algébrique impose aux élèves de traiter simultanément différentes informations complexes. Un tel raisonnement impose une charge cognitive élevée et met à l’épreuve la mémoire de travail, ce qui peut interférer avec la capacité d’apprentissage des élèves.
Cette exigence peut limiter leur capacité à développer de nouvelles connaissances, d’autant plus qu’ils peuvent ne pas centrer leur attention sur les informations pertinentes n’ayant pas encore développé les schémas adéquats.
Notion de problème résolu en algèbre
Un problème résolu est un énoncé accompagné de sa résolution complète et détaillée. Il montre à la fois le problème et les étapes utilisées pour établir une solution.
Un problème résolu peut être issu du travail de la production d’anciens élèves, de ressources pédagogiques, ou être généré directement par l’enseignant. Un problème résolu doit être aisément compréhensible par les élèves. Il présente le niveau de structure et de formalisme attendu de leur part à l’issue des apprentissages.
Les problèmes résolus vont minimiser la charge cognitive du raisonnement abstrait en permettant aux élèves d’avoir accès d’emblée à la solution complète devant leurs yeux. Ils peuvent analyser la résolution de manière détaillée et centrer leur attention de manière isolée sur chacune des différentes étapes de son établissement.
Les élèves ne doivent pas déterminer et exécuter chaque étape par eux-mêmes, ce qui a valeur de modélisation et va les aider à apprendre plus efficacement. C’est l’équivalent du modelage en enseignement explicite.
L’analyse et la discussion menées en classe autour des problèmes résolus peuvent également aider les élèves à mieux comprendre les processus logiques de raisonnement algébrique utilisés pour les résoudre.
De même, l’utilisation de problèmes résolus incomplets ou incorrects peut encourager les élèves à faire preuve d’esprit critique.
Les problèmes résolus complètent le modelage. Ils vont essentiellement intervenir lors de la pratique guidée dans une démarche d’enseignement explicite. Ils constituent également des ressources que les élèves pourront consulter en cas de nécessité lors de la pratique autonome.
Un exemple de problème résolu :
1. Étudier les stratégies et la structure des problèmes résolus en algèbre
L’enjeu pour l’enseignant est d’engager les élèves à discuter des structures et des solutions des problèmes résolus. De cette manière, ils peuvent établir des liens entre les stratégies et le raisonnement mis en œuvre.
Comprendre les stratégies mobilisées
Dans notre pratique en classe, nous devons offrir à nos élèves des occasions de discuter et d’analyser les problèmes résolus. Pour cela, nous leur demandons de décrire les étapes suivies dans le problème résolu et d’expliquer le raisonnement utilisé.
Nous posons aux élèves des questions spécifiques sur la stratégie de résolution. Nous leur demandons si cette stratégie est logique et mathématiquement correcte. Ces questions encouragent l’engagement actif des élèves.
Nous varions les questions en fonction des besoins des élèves et des types de problèmes abordés. Les questions peuvent être posées verbalement ou écrites afin que les élèves puissent s’y référer.
Questions pour faciliter la discussion sur la stratégie de résolution
Certaines questions générales peuvent s’appliquer à de nombreux types de problèmes d’algèbre :
- Quelles étaient les étapes de la résolution du problème ?
- Pourquoi sont-elles dans cet ordre ? Est-ce qu’elles fonctionneraient dans un ordre différent ?
- Le problème aurait-il pu être résolu avec moins d’étapes ?
- Quelqu’un peut-il imaginer une autre façon de résoudre ce problème ?
- Cette stratégie fonctionnera-t-elle toujours ? Pourquoi ?
- Quels sont les autres types de problèmes pour lesquels cette stratégie fonctionne ?
- Comment pouvons-nous modifier le problème donné de telle manière que cette stratégie ne fonctionne plus ?
- Comment pouvons-nous modifier ou exprimer la solution pour la rendre plus claire et accessible ?
- Quels concepts mathématiques sont liés à cette solution ?
Comprendre la structure de la résolution
La structure représente les caractéristiques et les relations mathématiques sous-jacentes d’une expression, d’une représentation ou d’une équation.
La structure comprend les quantités, les variables, les opérations et les relations (y compris l’égalité et l’inégalité). Les structures plus complexes sont construites à partir de structures simples. Reconnaître la structure implique la capacité de passer d’un niveau de complexité à un autre.
Nous pouvons favoriser une analyse approfondie des problèmes résolus en demandant aux élèves de remarquer et d’expliquer les différents aspects de la structure d’un problème.
L’examen attentif et la discussion de la structure et de chaque étape de la solution d’un problème résolu aident les élèves à reconnaître la nature séquentielle d’une résolution. Cela leur permet d’anticiper l’étape suivante de la résolution d’un problème. Cela peut améliorer la capacité des élèves à comprendre le raisonnement qui sous-tend les différentes stratégies de résolution de problèmes.
Questions pour faciliter la discussion sur la structure des problèmes
Certaines questions générales peuvent s’appliquer à de nombreux types de problèmes d’algèbre :
- Quelles sont les quantités — y compris les nombres et les variables — présentes dans ce problème ?
- Ces quantités sont-elles discrètes ou continues ?
- Quelles opérations et relations entre les quantités, le problème implique-t-il ?
- Y a-t-il des relations multiplicatives ou additives ?
- Le problème comporte-t-il une égalité ou une inégalité ?
2. Choisir des problèmes résolus qui reflètent l’objectif pédagogique et illustrent des erreurs courantes en algèbre
Nous choisissons des problèmes résolus qui sont liés aux objectifs d’apprentissage à partir d’exemples d’élèves, issus de ressources pédagogiques, ou en inventant ces exemples.
Des types spécifiques de problèmes résolus — problèmes différents résolus avec des étapes de solution similaires et problèmes résolus incorrects — peuvent être utilisés pour des objectifs d’apprentissage spécifiques.
Lors de la pratique autonome, nous permettons aux élèves de consulter les problèmes résolus, seuls ou en groupes, afin de comprendre les différentes manières de résoudre un problème lorsqu’ils ne sont pas sûrs de la marche à suivre.
Exemples de problèmes résolus pour différents objectifs d’apprentissage
Nous pouvons utiliser des problèmes résolus pour atteindre divers objectifs d’apprentissage.
Objectif 1 : résoudre un système d’équations à deux inconnues
En italique sont intégrées des questions pour guider la discussion avec les élèves.
Résoudre le système d’équations suivant :
2x – 4y = 10
5x – 2y = 9
Réponse de l’élève :
2x – 4y = 10
2x = 10 + 4y
x = 5 + 2y
Qu’est-ce qui a été fait en premier ? Pourquoi ? Cette première étape a-t-elle un sens ? Quelqu’un peut-il imaginer une première étape différente pour résoudre ce problème ?
5x – 2y = 9
5 (5 + 2y) – 2y = 9
25 + 10y – 2y = 9
25 + 8y = 9
8y = –16
y = –2
Qu’est-ce qui a été fait ensuite ? Pourquoi ? Est-ce que toutes ces étapes ont un sens ? Quelqu’un peut-il imaginer une autre façon de résoudre y ?
x = 5 + 2 (–2)
x = 5 + (–4)
x = 1
Comment x est-il résolu ? Cette stratégie fonctionnera-t-elle toujours ? Pourquoi ? Quelqu’un peut-il imaginer une autre façon de résoudre x ?
Vérification de la solution :
2 (1) – 4 (–2) = 10
2 – (–8) = 10
5 (1) – 2 (–2) = 9
5 – (–4) = 9
Les solutions sont-elles correctes ? Comment savons-nous qu’il n’y a pas d’erreurs ? Comment pouvons-nous savoir s’il y a des erreurs de raisonnement ? La stratégie utilisée fonctionnera-t-elle toujours ? Les étapes suivies fonctionneraient-elles dans un autre ordre ? Les équations auraient-elles pu être résolues de manière plus simple ou avec moins d’étapes ?
Objectif 2 : factoriser une expression quadratique
Qu’est-ce qui a été fait en premier ? Pouvons-nous expliquer pourquoi cela a été fait en premier ?Pourquoi avoir factorisé un 2 ? Quelqu’un peut-il penser à une autre façon de factoriser cette expression ? Comment vérifier la réponse ?
Exemples de problèmes résolus avec des degrés de difficulté variables
La présentation de plusieurs problèmes résolus qui utilisent des étapes de solution similaires peut aider les élèves à voir comment aborder différents problèmes dont la structure est similaire.
Pour intégrer plusieurs problèmes résolus dans une leçon, nous pouvons envisager les approches suivantes :
- Sélectionner des problèmes présentant différents niveaux de difficulté d’un même concept et les classer des plus simples aux plus complexes.
- Afficher les multiples exemples simultanément pour encourager les élèves à reconnaître des modèles dans les étapes de résolution des différents problèmes.
- Montrer les problèmes individuellement, l’un après l’autre, pour faciliter une discussion plus détaillée sur chaque problème.
Les deux lignes ci-dessous contiennent plusieurs problèmes résolus pour un sujet spécifique. Dans chaque rangée, les exemples vont du plus simple, à gauche, au plus difficile, à droite.
Factorisation :
Opérations sur la fonction :
Considérant les fonctions suivantes
Après avoir examiné les problèmes résolus corrects, nous pouvons utiliser les problèmes résolus incorrects pour aider les élèves à approfondir leur compréhension des concepts et des stratégies de solution correctes. Nous leur demandons d’analyser des erreurs de stratégie, de raisonnement et de procédure.
Les élèves peuvent discuter des problèmes et des stratégies qu’ils reconnaissent comme incorrects afin de mieux comprendre le processus utilisé pour obtenir une solution correcte.
Un mode d’introduction de problèmes résolus incorrects
- Nous pouvons donner aux élèves des problèmes résolus corrects à étudier et à discuter.
- Une fois que les élèves ont compris les stratégies et les problèmes corrects, nous leur présentons un problème résolu incorrect.
- Nous affichons le problème résolu de manière incorrecte, seul ou à côté d’une version correcte du même problème.
- Nous indiquons clairement que le problème a été résolu de manière incorrecte.
- Nous engageons une discussion sur l’erreur et les étapes qui ont conduit à la mauvaise réponse.
Lorsqu’ils analysent un problème résolu de manière incorrecte, les élèves doivent expliquer pourquoi les erreurs identifiées ont conduit à une réponse incorrecte afin de mieux comprendre les processus et stratégies corrects.
Nous présentons un problème résolu de manière incorrecte, seul ou à côté du même problème résolu correctement. Nous demandons aux élèves de comparer les deux stratégies utilisées. Nous identifions clairement les exemples corrects et incorrects, afin que les élèves ne confondent pas les stratégies correctes et incorrectes.
Une option, comme le montre l’exemple ci-dessous, consiste à montrer un problème résolu correctement à côté de plusieurs problèmes résolus incorrectement. Nous posons des questions d’approfondissement pour attirer l’attention des élèves sur les erreurs et les aider à comprendre ce qui n’a pas été fait correctement.
Exemples de questions pour guider la discussion sur les erreurs :
- Comment peux-tu montrer que les réponses des élèves B et C sont incorrectes ?
- Quels conseils donnerais-tu aux élèves B et C pour les aider à éviter de factoriser incorrectement ce type de problème à l’avenir ?
- Comment peux-tu vérifier que l’élève A a factorisé cette expression correctement ?
- Quelle stratégie utiliserais-tu pour factoriser cette expression et pourquoi as-tu choisi cette stratégie ?
Nous pouvons faire figurer différents types d’erreurs à côté d’un problème résolu correct.
Les erreurs peuvent résulter de l’utilisation d’une stratégie incorrecte (erreur de stratégie ou de raisonnement) ou d’une erreur dans les opérations mathématiques (erreur de procédure ou de calcul). Nous encourageons nos élèves à réfléchir de manière critique à la façon dont différentes étapes et différents choix peuvent conduire à des erreurs.
3. Utiliser des discussions en classe entière, des travaux en petits groupes et des activités de pratique indépendante pour présenter, développer et pratiquer avec des problèmes résolus dans le cadre de l’algèbre
Les problèmes résolus sont utiles dans une variété de contextes.
Nous pouvons introduire des problèmes résolus pendant l’enseignement en classe entière pour donner un aperçu d’une stratégie de solution. Par exemple, après avoir commencé à expliquer la forme de l’ordonnée à l’origine, nous pouvons utiliser les problèmes résolus pour introduire le concept de représentation graphique des équations linéaires.
Exemple d’utilisation de problèmes résolus dans le cadre d’une discussion en classe entière
Question :
Nous utilisons alors les questions de la colonne de droite pour guider l’analyse et la discussion des élèves sur le problème résolu.
| La pente d’une droite est de -0,5. Le point (6, 8) est situé sur la droite. Quelle est l’équation de la droite ? Quelle est l’ordonnée à l’origine ? Tracez un graphique de cette ligne. |
|
| Réponse de l’élève | Questions pour la discussion en classe |
y = mx + p |
Graphiquement, que représentent m et p ? |
y = -0,5 x + p |
Qu’est-ce que l’élève a fait en premier ? Pourquoi ? Qu’est-ce que -0,5 représente ? Quelqu’un peut-il penser à une première étape différente pour résoudre cette équation ? |
8 = -0,5 (6) + p 8 = - 3 + p 8 + 3 = p p = 11 |
Qu’a fait l’élève dans cette série d’étapes ? Pourquoi est-il important de résoudre p ? Que pouvons-nous en conclure graphiquement ? |
y = -0,5 x + 11 L’ordonnée à l’origine vaut 11. La pente est de -0,5. |
Comment l’élève a-t-il obtenu cette équation ? Comment pouvons-nous savoir que cette équation est correcte ? Le point (6, 8) est-il situé sur cette ligne ? La droite passe-t-elle par le point (6, 8) ? Explique comment tu le sais. Quelles conditions sont données dans le problème ? Comment le graphique répond-il à ces conditions ? Une autre droite est-elle possible ? Pourquoi ou pourquoi pas ? |
Nous pouvons créer des activités permettant à des paires ou à de petits groupes d’élèves d’analyser de manière critique les problèmes résolus.
Par exemple, nous présentons des problèmes résolus, y compris une combinaison de problèmes résolus incorrects et corrects, accompagnés de questions auxquelles les élèves doivent répondre en petits groupes de deux ou trois personnes.
Les questions peuvent porter sur les étapes, les structures et les stratégies des problèmes résolus. Une fois que les élèves ont travaillé en petits groupes, réunissez toute la classe pour discuter plus avant des problèmes en utilisant un langage mathématiquement approprié, et nous invitons tous les élèves à aborder les éléments pertinents du problème.
Exemple de problèmes résolus dans le cadre d’un travail en petits groupes
Les élèves peuvent travailler avec un partenaire ou en petits groupes pour étudier ces problèmes résolus et répondre aux questions.
Résoudre l’équation suivante :
Nous allons supposer que 8 x + 10 est différent de 0.
Voici une résolution correcte :
- Qu’est-ce que l’élève a fait en premier pour résoudre l’équation ?
- Cette première étape était-elle appropriée pour résoudre cette équation ? Pourquoi ou pourquoi pas ?
- Comment les priorités des opérations sont-elles respectées ?
- Comment l’élève a-t-il raisonné pour résoudre ce problème ?
- Comment montrer que l’élève a trouvé la bonne solution à l’équation ?
Cet élève n’a pas résolu cette équation correctement :
- Qu’a-t-il fait en premier pour résoudre l’équation ?
- Cette première étape était-elle appropriée pour résoudre cette équation ? Pourquoi ou pourquoi pas ?
- Comment l’élève a-t-il raisonné pour résoudre ce problème ?
- Quelle erreur a-t-il commise ?
- Quelle stratégie pourrais-tu utiliser pour résoudre correctement cette équation ?
Les problèmes résolus peuvent remplacer certains exercices dans la pratique autonome des élèves. Nous pouvons donner aux élèves des problèmes résolus incomplets et leur demander de compléter les solutions.
Exemple de problèmes résolus incomplets
Nous incluons des problèmes résolus incomplets dans la pratique autonome des élèves, en leur demandant de compléter les étapes vides des problèmes résolus.
Dans les problèmes résolus incomplets, nous déterminons quelle étape du problème doit rester vide, en fonction du degré de familiarité des élèves avec le sujet et des intentions d’apprentissage.
Une autre stratégie pour intégrer des problèmes résolus dans des activités de pratique indépendante consiste à alterner des problèmes résolus avec des problèmes non résolus. Ces derniers sont similaires aux problèmes résolus en matière de structure de problème ou de stratégie de solution.
Nous créons des exercices qui présentent un problème résolu, suivi d’un problème non résolu que les élèves doivent résoudre. Les élèves peuvent utiliser le problème résolu comme exemple pour guider leur travail indépendant, tandis que le problème non résolu leur permet de s’engager activement dans le problème résolu.
Exemple de pratique indépendante intégrant des problèmes résolus
Nous donnons à nos élèves des problèmes à compléter aux élèves pour qu’ils s’entraînent de manière autonome.
Nous leur demandons d’étudier d’abord le problème résolu dans la colonne de gauche, puis de développer les expressions dans la colonne de droite de chaque ligne.
Nous encourageons nos élèves à remarquer les étapes utilisées dans le problème résolu et nous leur expliquons que ces étapes sont similaires à celles qu’ils devront utiliser pour résoudre les expressions de la colonne de droite. Nous demandons à nos élèves de montrer comment ils ont trouvé leurs solutions aux problèmes de la colonne de droite et de réfléchir à la manière dont ils pourraient montrer à un autre élève que leurs solutions sont correctes.
Obstacles potentiels et approches suggérées
Mais tous les enseignants font déjà ça !
Utiliser des exemples lors de la phase d’enseignement en mathématiques et un lieu commun, ce qui change ici est l’aspect systématique, préventif, proactive et hautement interactif de la démarche.
Nous devons nous assurer que tous nos élèves y participent pleinement. La discussion et l’analyse des problèmes résolus en classe entière peuvent aider tous les élèves à remarquer les aspects importants des problèmes résolus.
Le fait de poser des questions à tous les élèves et de favoriser la discussion les encourage à réfléchir de manière critique et autonome aux problèmes résolus. Pendant l’enseignement en classe entière, nous devons montrer aux élèves comment s’impliquer pleinement dans les problèmes résolus par un modelage et en exprimant nos propres processus de réflexion à haute voix.
Nous devons rechercher toutes les occasions d’intégrer les problèmes résolus dans de nombreux aspects de nos cours, au-delà de l’enseignement en classe entière et d’engager nos élèves dans des traitements actifs de ceux-ci :
- Dans le cadre d’un travail en petits groupes ou en autonomie, nous devons amener nos élèves à s’intéresser aux problèmes résolus de manière plus significative.
- Plutôt que de simplement les laisser étudier de problèmes résolus en les lisant ou en les recoupant, nous engageons nos élèves dans des questions d’approfondissement.
- Nous leur demandons de compléter les étapes manquantes de problèmes résolus incomplets ou de résoudre eux-mêmes des problèmes après avoir étudié un problème résolu similaire.
- Les évaluations formatives en classe peuvent également demander aux élèves d’analyser les problèmes résolus de la même manière qu’ils ont été intégrés dans les leçons.
Je n’ai pas les problèmes résolus adéquats pour enseigner comme ça !
Certains enseignants peuvent ne pas savoir où trouver des problèmes résolus adéquats à utiliser dans leur classe où n’ont pas le temps matériel de créer par eux-mêmes suffisamment de nouveaux exemples pour leurs cours.
Les problèmes résolus peuvent provenir de nombreuses sources. Souvent, les ressources pédagogiques ou les manuels scolaires peuvent inclure un certain nombre d’exemples ou des problèmes résolus. En outre, des travaux ou des évaluations antérieures d’élèves peuvent fournir des problèmes résolus.
Ces derniers peuvent également fournir des exemples de problèmes résolus, notamment en ce qui concerne les erreurs stratégiques, procédurales ou calculatoires courantes ou les conceptions erronées.
De plus, l’enseignant peut collaborer avec ses collègues pour échanger et récolter des exemples de problèmes résolus. Il peut mener avec eux la réflexion sur leur exploitation dans le cadre d’une communauté d’apprentissage professionnelle et du travail collaboratif.
C’est dangereux de montrer des erreurs aux élèves, car ils vont les retenir !
Intuitivement, nous pourrions craindre que le fait de montrer aux élèves des problèmes résolus incorrects puisse leur faire apprendre des erreurs.
En réalité, le fait de faire analyser par nos élèves des problèmes incorrectement résolus a pour enjeu de les aider à comprendre la différence entre les stratégies de résolution correctes et incorrectes. Cela peut mettre en évidence le raisonnement derrière les erreurs courantes. Ils deviendront capables de détecter ces erreurs et de les prévenir, car ils apprennent mieux le raisonnement sous-jacent.
Nous permettons également à nos élèves de comprendre que la compréhension du processus est aussi importante que l’obtention de la réponse correcte finale.
De plus, les problèmes résolus incorrects sont toujours clairement identifiés, afin que les élèves reconnaissent qu’il y a une erreur dans les étapes de la solution. La présentation de problèmes résolus corrects en parallèle avec des problèmes résolus incorrects peut aider les élèves à reconnaître et à analyser l’erreur.
De même, il est important pour l’enseignant de s’engager dans une discussion avec les élèves sur chaque étape du problème résolu de manière incorrecte. Il leur explique en détail la nature de l’erreur dans un dialogue formatif. Son objectif est de réduire la confusion quant aux stratégies appliquées correctement et incorrectement.
Les élèves qui sont en mesure d’identifier et de discuter les raisons de l’existence d’une erreur acquièrent des avantages. En toute logique, ils seront peut-être mieux à même de reconnaître quand et comment utiliser les bonnes stratégies lorsqu’ils résoudront des problèmes de manière autonome.
De manière générale, les élèves n’ont pas l’habitude d’analyser leur travail et d’interpréter les mathématiques. Or la capacité de se relire est une démarche de base de l’autorégulation fondamentale à la pratique autonome. En amenant à nos élèves à analyser des problèmes résolus, nous leur apprenons à se relire eux-mêmes et à vérifier spontanément leurs productions. Ils acquièrent de bonnes habitudes productives en mathématiques. La discussion sur les problèmes résolus de manière incorrecte permet aux élèves de se confronter à leurs propres erreurs potentielles de manière non menaçante.
De même, lorsqu’ils évaluent un travail d’élève hypothétique, les élèves peuvent être plus ouverts et honnêtes dans leur analyse des erreurs qu’ils ne le seraient s’ils critiquaient leur propre travail.
Mis à jour le 24/02/2025
Bibliographie
Star, J. R., Caronongan, P., Foegen, A., Ferguson, J., Keating, B., Larson, M. R., et al. (2015). Teaching strategies for improving algebra knowledge in middle and high school students (NCEE 2014–4333). Washington, DC: National Center for Education Evaluation and Regional Assistance (NCEE), Institute of Education Sciences, U.S. Department of Education. Retrieved from: https://ies.ed.gov/ncee/wwc/PracticeGuides









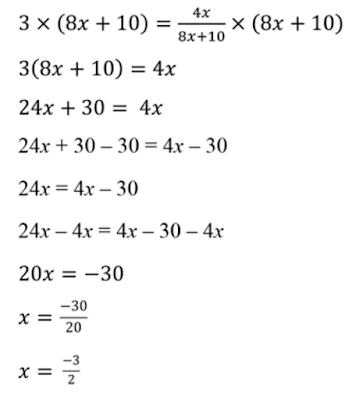



0 comments:
Enregistrer un commentaire