(Photographie : Eric Pawlitzky)
- Voir article : L’effet du problème résolu et du problème à compléter
Approche traditionnelle ou constructiviste de l’apprentissage de la résolution de problèmes
Traditionnellement, dans un cours de mathématiques ou de sciences (chimie ou physique), un enseignant démarre par une mise en situation, puis modélise la nouvelle matière, agrémentée d’exemples simples d’application.
Les cours traditionnels sont généralement structurés de telle sorte que les élèves reçoivent d’abord quelques exemples de solutions correctes aux types de problèmes qu’ils vont apprendre, tout en recevant l’explicitation des divers concepts et règles.
Ces exemples peuvent être élaborés par l’enseignant au tableau ou imprimés au début du chapitre du manuel.
Les élèves et l’enseignant peuvent essayer de résoudre quelques problèmes ensemble. Ensuite, l’élève est invité à pratiquer les techniques sur une liste de problèmes de complexité croissante qu’il doit résoudre lui-même ou en petits groupes.
Les élèves se retrouvent ensuite à s’entrainer à résoudre de longues séries de problèmes et d’exercices par eux-mêmes, soit en classe, soit chez eux sous forme de devoirs. Généralement, ils ne reçoivent la correction des exercices qu’après avoir essayé avec ou sans succès d’y répondre.
Enseignement explicite de l’apprentissage de la résolution de problèmes
Dans le cadre d’une démarche d’enseignement explicite, l’usage de problèmes résolus est nettement plus développé. Au contraire de traditionnels exemples, les enseignants vont explorer une plus grande variété de situations simples à complexes. Ils vont également accompagner les élèves de manière plus structurée dans une acquisition de la compétence visée.
Cela démarre par de la pratique guidée puis se poursuit par une pratique autonome. Enfin cela se poursuit grâce à une pratique distribuée dans le temps sous forme de révisions, de devoirs, d’évaluations formatives ou de quiz qui permettent d’entrainer les élèves à la récupération.
L’enseignement explicite suggère comme alternative à la résolution directe de problème l’intégration nette de problèmes résolus que les élèves peuvent observer, imiter, compléter, analyser ou vérifier afin d’apprendre plus efficacement.
De nombreuses recherches en laboratoire et en contexte de classe suggèrent que l’étude de problèmes résolus améliore de manière notable l’apprentissage des élèves pour les cours de mathématiques et de sciences.
En apprenant à partir de problèmes résolus, les élèves vont développer bien plus rapidement et plus efficacement les savoirs, savoir-faire et compétences attendues.
Les problèmes résolus peuvent être utilisés de différentes manières pour différents objectifs éducatifs. Ce sont ces différentes pistes qui seront explorées.
Usage basique du problème résolu
Il s’agit de donner aux élèves des problèmes résolus puis leur donner d’autres problèmes similaires à résoudre qui demandent de mobiliser les mêmes démarches.
Selon le principe du problème résolu, il est préférable de remplacer certains des problèmes pratiques donnés dans le cadre d’un enseignement traditionnel ou constructiviste par des exemples de solutions élaborées.
Nous demandons aux élèves d’observer, d’analyser et d’étudier les procédures de solutions au lieu d’essayer de résoudre ces problèmes par eux-mêmes directement (figure 1).
Cette approche est jugée bénéfique, car elle met l’accent sur les capacités cognitives des élèves :
- Leurs ressources en mémoire de travail sont limitées.
- Ils ne peuvent pas encore se reposer sur leur mémoire à long terme en ce qui concerne de nouveaux problèmes. Ils ne disposent pas encore des modèles mentaux pour comprendre les stratégies spécifiques de résolution correcte des problèmes dans le domaine considéré.
Lorsque les élèves s’essaient à résoudre des problèmes pratiques par eux-mêmes, ils devinent souvent quelles procédures de résolution de problèmes peuvent être appropriées par une stratégie moyens-fins et s’exercent ensuite à les appliquer. Le processus n’assure pas à coup sûr un apprentissage. Il se révèle lent, inefficace et susceptible de fixer des erreurs.
Le fait de donner des problèmes résolus à étudier avant de demander aux élèves de s’engager dans la résolution de cas similaires est bénéfique. La démarche améliore la capacité des élèves à résoudre des problèmes très similaires à ceux qu’ils ont étudiés ainsi que des problèmes plus difficiles que ceux qu’ils ont étudiés. Cette approche permet régulièrement d’apprendre la même chose en moins de temps ou d’en apprendre davantage.
Les problèmes à compléter
Les élèves ont un statut de novices pour l’essentiel des contenus que nous leur enseignons en mathématiques et en sciences.
Lorsque nous sommes entièrement novices pour une matière, nous tirons davantage profit des problèmes résolus que d’essayer de les résoudre d’emblée. La situation s’inverse lorsque les savoirs et savoir-faire pour une matière ont été appris et automatisés.
Dès lors, il y a intérêt à intensifier l’intégration des problèmes résolus dans la pratique des élèves, car ils sont avant tout des novices.
Une approche pédagogique utile consiste à augmenter puis à faire disparaître dans un second temps, le soutien apporté aux élèves grâce à des problèmes résolus. Nous retirons l’étayage au fur et à mesure que la pratique se poursuit et que les élèves deviennent plus compétents.
L’enseignant fournit des problèmes résolus à ses élèves, mais ceux-ci sont de moins en moins résolus au fil du temps. L’élève complète les parties manquantes de la résolution par lui-même.
Lorsque nous utilisons le principe du problème à compléter, le premier ou les premiers exemples sont complètement résolus. Pour le suivant, l’élève doit compléter une étape.
Au fur et à mesure, les problèmes suivants comportent de moins en moins d’étapes développées et résolues, et de plus en plus d’étapes que les élèves doivent compléter eux-mêmes (figure 2).
Ce type d’étayage est censé aider les élèves à passer sans heurts des problèmes résolus à la résolution complète de problèmes par eux-mêmes. De cette manière, les apprentissages suivent une progression. Au fur et à mesure que l’élève développe ses connaissances, il devient plus apte à faire face à des problèmes plus exigeants. Ainsi, la complexité des tâches demandées en matière de résolution de problèmes augmente progressivement. De cette manière, les capacités cognitives des élèves sont continuellement sollicitées sans jamais que leurs limites soient dépassées. L’élève ne se trouve jamais dans une impasse comme c’est régulièrement le cas lors de l’utilisation traditionnelle des problèmes résolus.
L’utilisation de l’approche des problèmes à compléter permet de meilleures performances d’apprentissage sur des catégories de problèmes difficiles, à la fois en matière de temps nécessaire et de niveau de performance. Des étudiants qui travaillent avec des problèmes à compléter ont moins de moments improductifs pendant une séance de pratique.
L’apprentissage s’améliore davantage lorsque les étapes du problème à compléter le sont à partir de la fin de la résolution du problème plutôt qu’à partir de son début.
De plus, lorsqu’il est possible d’adapter la diminution de l’étayage spécifiquement en fonction des progrès des élèves, en le réduisant au moment optimal, il a été démontré que les avantages sont plus importants.
Les problèmes résolus et l’auto-explication
L’auto-explication consiste à amener les élèves à s’expliquer ce qu’ils comprennent et retiennent pendant qu’ils lisent ou étudient.
Les meilleurs élèves ont tendance à s’expliquer naturellement. Il a été démontré que le fait d’inciter tous les élèves à s’expliquer facilite l’intégration de nouvelles informations aux connaissances antérieures. Cela va rendre les nouvelles connaissances plus explicites, accessibles et mémorables.
Dans le cadre de problèmes résolus, il est demandé aux élèves d’expliquer ce qui a été fait dans l’exemple ou pourquoi les étapes démontrées sont correctes (figure 3).
L’auto-explication liée à des problèmes résolus augmente :
- Les connaissances déclaratives
- La capacité de transfert des connaissances considérées
- La probabilité d’identifier les informations pertinentes dans un problème
- La compréhension des concepts sous-jacents aux problèmes
- La capacité à réaliser par la suite les étapes considérées.
Les problèmes résolus incorrects
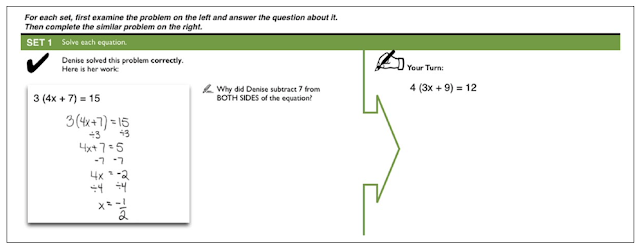
Des exemples de solutions de problèmes incorrectes, soit en conjonction avec des exemples corrects, soit à la place de ceux-ci sont fournis aux élèves. (figure 4)
Les problèmes résolus incorrects sont identifiés comme tels. Idéalement, ils exposent une erreur courante que les élèves tendent à faire lors de leur apprentissage.
L’explication des erreurs est censée aider les élèves à déterminer quelles caractéristiques du problème rendent l’étape spécifique franchie incorrecte. Cela peut aider les élèves à corriger leurs connaissances erronées et à affiner leurs stratégies de résolution de problèmes de manière à se prémunir contre ces erreurs en y devenant attentifs.
L’usage de problèmes résolus incorrects encourage l’apprentissage de concepts et de procédures corrects, réduit les idées fausses et peut conduire à une meilleure compréhension conceptuelle du contenu.
Les élèves ayant des connaissances préalables élevées tirent un plus grand bénéfice des problèmes résolus incorrects, mais en fonction des études, ces avantages peuvent s’étendre aux élèves ayant des connaissances préalables faibles également.
Nous pouvons aider les élèves ayant des connaissances préalables faibles à tirer profit des exemples résolus incorrects. Pour cela, nous pouvons mettre en évidence la partie de la solution dans laquelle l’erreur s’est produite afin qu’ils n’aient pas à localiser l’erreur eux-mêmes. Ils peuvent alors pleinement utiliser leur temps pour l’analyser et l’expliquer.
La comparaison de problèmes résolus
Nous présentons simultanément deux problèmes résolus aux élèves et à demandons aux élèves de les comparer. En général, le processus de comparaison favorise un apprentissage significatif des concepts sous-jacents et des catégories de contenu. (Figure 5)
Cependant, il existe de nombreuses possibilités de comparaison :
- La comparaison de solutions isomorphiques correctes pour deux problèmes du même type
- La comparaison de solutions correctes pour deux types de problèmes distincts
- La comparaison d’une solution incorrecte pour un problème à une solution correcte pour le même problème
- La comparaison de deux solutions correctes alternatives pour le même problème.
Le plus intéressant est le quatrième type. Nous montrons aux élèves deux solutions différentes, mais correctes, au même problème. Nous leur demandons de les comparer et de déterminer quelle est la meilleure stratégie de solution (voir figure 6).
La comparaison de méthodes alternatives conduit à une plus grande flexibilité procédurale. Les élèves connaissent alors plusieurs méthodes pour résoudre un problème et choisissent la plus efficace compte tenu du contexte du problème.
Cette approche aide les élèves à mieux identifier les aspects critiques des solutions aux problèmes afin d’envisager la stratégie la plus adéquate pour résoudre un problème.
Il apparaît que les élèves peuvent avoir besoin d’avoir atteint un seuil de connaissances préalables avant de pouvoir bénéficier pleinement de l’étude de méthodes alternatives. L’avantage supplémentaire est plus perceptible pour les élèves de meilleur niveau.
Repenser les supports pédagogiques et la formation des enseignants pour intégrer de l’effet du problème résolu
Repenser les manuels de sciences et de mathématiques
Les recherches sur les problèmes résolus montrent que la façon dont les manuels scolaires en mathématiques et en sciences sont structurés est sous-optimale pour l’apprentissage des élèves.
Les manuels traditionnels comprennent des exemples pendant les pages explicitant la théorie, suivis de listes de problèmes pratiques. Si des problèmes résolus sont présents, ils sont trop peu nombreux et ne sont pas utilisés efficacement.
Les recherches sur les problèmes résolus suggèrent qu’environ la moitié des problèmes dans un manuel devrait présenter une solution que les élèves pourraient étudier.
Le manque d’exemples concrets n’est pas le seul problème lié aux manuels scolaires. Nous pouvons également considérer un manque d’espacement et d’entremêlement des exercices à l’intérieur de ceux-ci.
Un autre souci est que les manuels scolaires comprennent souvent une variété d’images colorées, incluses à des fins esthétiques. Différentes études indiquent que des schémas pertinents pour le contenu soutiennent l’apprentissage des élèves. À l’opposé, des illustrations et des photographies colorées et décoratives peuvent nuire à l’apprentissage.
La formation des enseignants
La formation des enseignants ne favorise pas actuellement la mise en œuvre des problèmes résolus de manière efficace. Les enseignants sont assez peu formés à des approches comme l’enseignement explicite, la théorie de la charge cognitive ou la science de l’apprentissage qui contribuent à expliquer et à valoriser ce type d’approche.
Il existe des besoins en matière de développement professionnel des enseignants afin de les aider à comprendre pleinement les atouts que peut procurer une incorporation large de problèmes résolus dans l’apprentissage des sciences ou des mathématiques.
Usages optimaux de l’effet du problème résolu
Nous l’avons vu, il y a une variété de façons dont les problèmes résolus peuvent être utilisés en classe pour structurer le temps de pratique. L’efficacité de ces méthodes dépend de l’objectif de la leçon :
- Les leçons qui ciblent la fluidité procédurale peuvent intégrer des problèmes à compléter.
- Les leçons axées sur les concepts peuvent utiliser des problèmes résolus en lien avec l’auto-explication.
- Les leçons visant à corriger les idées fausses et conceptions erronées des élèves peuvent être axées sur des problèmes résolus incorrects.
- Les leçons encourageant la flexibilité dans la résolution des problèmes pourraient utiliser la comparaison de méthodes alternatives pour résoudre le même problème.
Mis à jour le 25/11/2023
Bibliographie
Booth, Julie & Mcginn, Kelly & Young, Laura & Barbieri, Christina. (2015). Simple Practice Doesn’t Always Make Perfect: Evidence From the Worked Example Effect. Policy Insights from the Behavioral and Brain Sciences. 2. 24–32. 10.1177/2372732215601691.






0 comments:
Enregistrer un commentaire